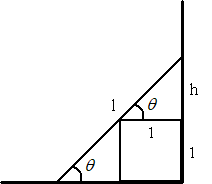
A ladder of length $l=2\sqrt 6$ unit is resting against a wall just touching the cube of edge 1 unit as shown in the figure. Find h above the cube.
Solution
We have, $\tan \theta = h$ and $\sin \theta = \frac{{h + 1}}{l}$
Solution
So, $2\sqrt 6 \sin \theta = 1 + \tan \theta $
$ \Rightarrow \sqrt 6 (2\sin \theta \cos \theta ) = \cos \theta + \sin \theta $
Squaring, ${(\sqrt 6 \sin 2\theta )^2} = {(\cos \theta + \sin \theta )^2}$
$ \Rightarrow 6{\sin ^2}2\theta = 1 + \sin 2\theta $
Let, $\sin 2\theta = t$
We have, $6{t^2} - t - 1 = 0$
$ \Rightarrow 6{t^2} - 3t + 2t - 1 = 0$
$ \Rightarrow 3t(2t - 1) + (2t - 1) = 0$
$ \Rightarrow (3t + 1)(2t - 1) = 0$
Thus, $t = \frac{1}{2} = \sin 2\theta $
[Since, $\sin 2\theta >0$ the other solution is rejected.]
$\therefore 2\theta = {30^ \circ },{150^ \circ }$
Or, $\theta = {15^ \circ },{75^ \circ }$
Now, $h = \tan \theta = \tan {15^ \circ },\tan {75^ \circ } = 2 \pm \sqrt 3 $